一文搞定深度学习建模预测全流程(Python)
扫描二维码
随时随地手机看文章

来源 | 算法进阶本文详细地梳理及实现了深度学习模型构建及预测的全流程,代码示例基于python及神经网络库keras,通过设计一个深度神经网络模型做波士顿房价预测。主要依赖的Python库有:keras、scikit-learn、pandas、tensorflow(建议可以安装下anaconda包,自带有常用的python库)
一、基础介绍
- 机器学习
- 深度学习
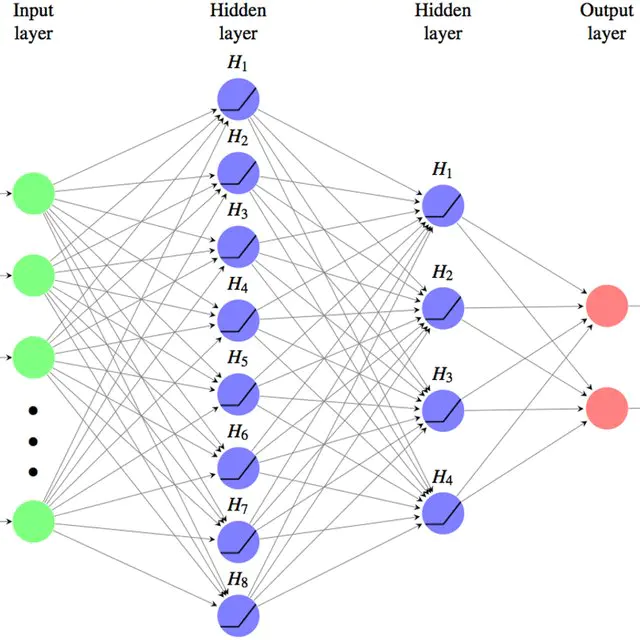
- keras简介

二、建模流程
深度学习的建模预测流程,与传统机器学习整体是相同的,主要区别在于深度学习是端对端学习,可以自动提取高层次特征,大大减少了传统机器学习依赖的特征工程。如下详细梳理流程的各个节点并附相应代码: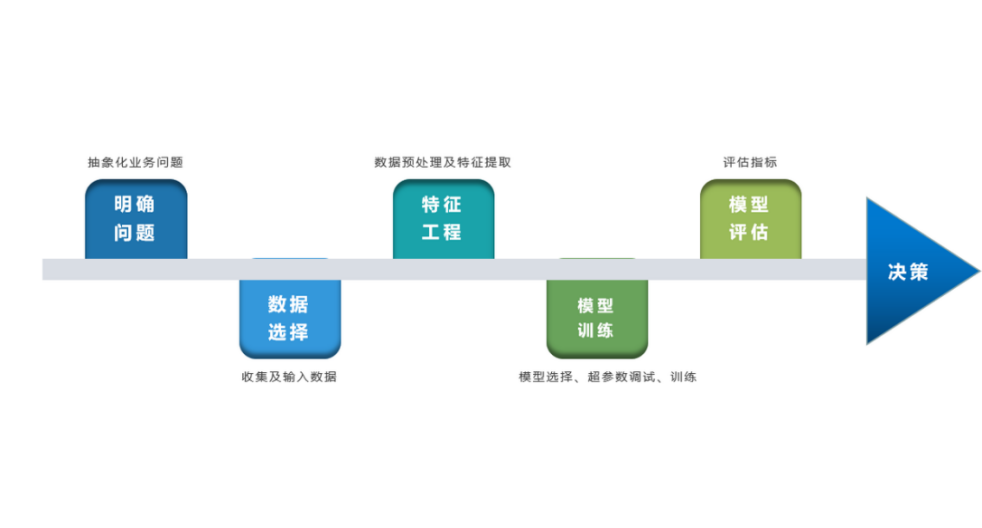
2.1 明确问题及数据选择
2.1.1 明确问题
深度学习的建模预测,首先需要明确问题,即抽象为机器 / 深度学习的预测问题:需要学习什么样的数据作为输入,目标是得到什么样的模型做决策作为输出。
2.1.2 数据选择
深度学习是端对端学习,学习过程中会提取到高层次抽象的特征,大大弱化特征工程的依赖,正因为如此,数据选择也显得格外重要,其决定了模型效果的上限。如果数据质量差,预测的结果自然也是很差的——业界一句名言“garbage in garbage out”。
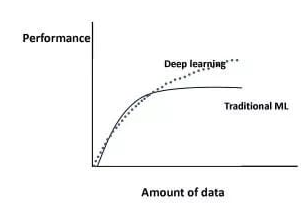 然而工程实践中,受限于硬件支持、标注标签成本等原因,样本的数据量通常是比较有限的,这也是机器学习的重难点。对于模型所需最少的样本量,其实没有固定准则,需要要结合实际样本特征、任务复杂度等具体情况(经验上,对于分类任务,每个类别要上千的样本数)。
然而工程实践中,受限于硬件支持、标注标签成本等原因,样本的数据量通常是比较有限的,这也是机器学习的重难点。对于模型所需最少的样本量,其实没有固定准则,需要要结合实际样本特征、任务复杂度等具体情况(经验上,对于分类任务,每个类别要上千的样本数)。
-
收集房价相关的数据信息(特征维度)和对应房价(标签),以及尽量多的样本数。数据信息如该区域的繁华程度、教育资源、治安等情况就和预测的房价比较相关,有代表性。而诸如该区域“人均养的兔子数”类数据信息,对房价的预测就没那么相关,对于无代表性的数据特征的加入,主要会增加人工处理的成本、计算复杂度,还有可能引入了模型学习的噪音。
-
划定好数据时间窗口。比如我们可以学习该区域历史2010~2020年的房价,预测未来2021的房价(这是一个经典的时间序列预测问题,常用RNN模型)。但却不能学习了2021年或者更后面的未来房价、人口数等相关信息,反过来去预测2021年房价,这就是一个数据泄露的问题(模型都学习了与标签相关等未知的信息,还预测个啥?)。
本节代码
如下加载数据的代码,使用的是keras自带的波士顿房价数据集。一些常用的机器学习开源数据集可以到kaggle.com/datasets、archive.ics.uci.edu等网站下载。
(train_x, train_y), (test_x, test_y) = boston_housing.load_data()
波士顿房价数据集是统计20世纪70年代中期波士顿郊区房价等情况,有当时城镇的犯罪率、房产税等共计13个指标(特征)以及对应的房价中位数(标签)。

2.2 特征工程
特征工程就是对原始数据分析处理,转化为模型可用的特征。这些特征可以更好地向预测模型描述潜在规律,从而提高模型对未见数据的准确性。对于深度学习模型,特征生成等加工不多,主要是一些数据的分析、预处理,然后就可以灌入神经网络模型了。
2.2.1 探索性数据分析
选择好数据后,可以先做探索性数据分析(EDA)去理解数据本身的内部结构及规律。如果你对数据情况不了解,也没有相关的业务背景知识,不做相关的分析及预处理,直接将数据喂给模型往往效果不太好。通过探索性数据分析,可以了解数据分布、缺失、异常及相关性等情况。
本节代码
我们可以通过EDA数据分析库如pandas profiling,自动生成分析报告,可以看到这份现成的数据集是比较"干净的":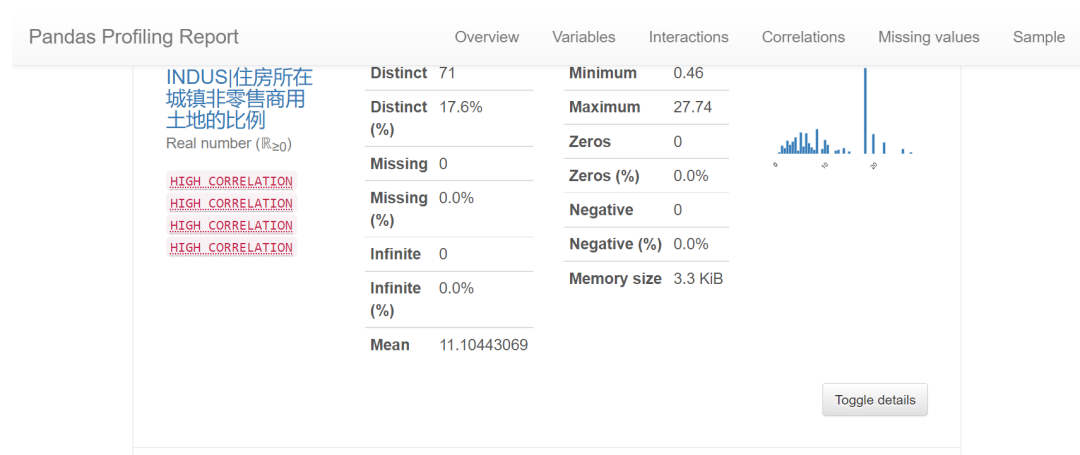
import pandas_profiling
# 特征名称
feature_name = ['CRIM|住房所在城镇的人均犯罪率',
'ZN|住房用地超过 25000 平方尺的比例',
'INDUS|住房所在城镇非零售商用土地的比例',
'CHAS|有关查理斯河的虚拟变量(如果住房位于河边则为1,否则为0 )',
'NOX|一氧化氮浓度',
'RM|每处住房的平均房间数',
'AGE|建于 1940 年之前的业主自住房比例',
'DIS|住房距离波士顿五大中心区域的加权距离',
'RAD|距离住房最近的公路入口编号',
'TAX 每 10000 美元的全额财产税金额',
'PTRATIO|住房所在城镇的师生比例',
'B|1000(Bk|0.63)^2,其中 Bk 指代城镇中黑人的比例',
'LSTAT|弱势群体人口所占比例']
train_df = pd.DataFrame(train_x, columns=feature_name) # 转为df格式
pandas_profiling.ProfileReport(train_df)
2.2.2 特征表示
像图像、文本字符类的数据,需要转换为计算机能够处理的数值形式。图像数据(pixel image)实际上是由一个像素组成的矩阵所构成的,而每一个像素点又是由RGB颜色通道中分别代表R、G、B的一个三维向量表示,所以图像实际上可以用RGB三维矩阵(3-channel matrix)的表示(第一个维度:高度,第二个维度:宽度,第三个维度:RGB通道),最终再重塑为一列向量(reshaped image vector)方便输入模型。
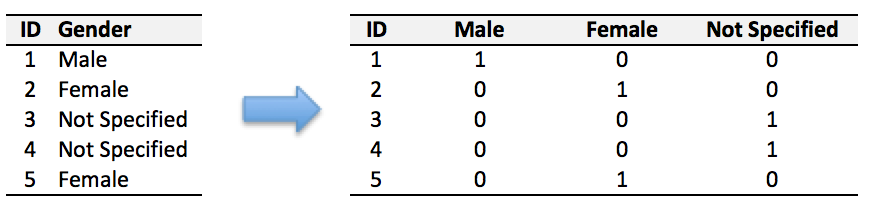
本节代码
数据集已是数值类数据,本节不做处理。
2.2.2 特征清洗
-
异常值处理 收集的数据由于人为或者自然因素可能引入了异常值(噪音),这会对模型学习进行干扰。通常需要处理人为引起的异常值,通过业务及技术手段(如数据分布、3σ准则)判定异常值,再结合实际业务含义删除或者替换掉异常值。
-
缺失值处理 神经网络模型缺失值的处理是必要的,数据缺失值可以通过结合业务进行填充数值或者删除。① 缺失率较高,结合业务可以直接删除该特征变量。经验上可以新增一个bool类型的变量特征记录该字段的缺失情况,缺失记为1,非缺失记为0;② 缺失率较低,可使用一些缺失值填充手段,如结合业务fillna为0或-9999或平均值,或者训练回归模型预测缺失值并填充。
本节代码
从数据分析报告可见,波士顿房价数据集无异常、缺失值情况,本节不做处理。
2.2.3 特征生成
特征生成作用在于弥补基础特征对样本信息的表达有限,增加特征的非线性表达能力,提升模型效果。它是根据基础特征的含义进行某种处理(聚合 / 转换之类),常用方法如人工设计、自动化特征衍生(如featuretools工具):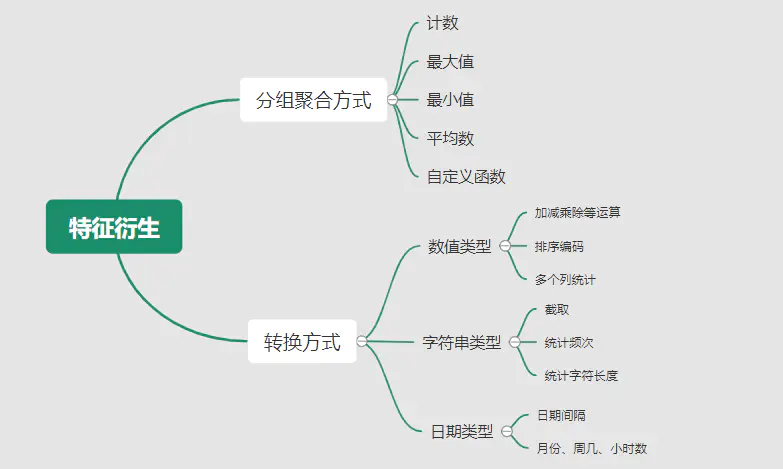 深度神经网络会自动学习到高层次特征,常见的深度学习的任务,图像类、文本类任务通常很少再做特征生成。而对于数值类的任务,加工出显著特征对加速模型的学习是有帮助的,可以做尝试。
深度神经网络会自动学习到高层次特征,常见的深度学习的任务,图像类、文本类任务通常很少再做特征生成。而对于数值类的任务,加工出显著特征对加速模型的学习是有帮助的,可以做尝试。
本节代码
特征已经比较全面,本节不再做处理,可自行验证特征生成的效果。
2.2.4 特征选择
特征选择用于筛选出显著特征、摒弃非显著特征。这样做主要可以减少特征(避免维度灾难),提高训练速度,降低运算开销;减少干扰噪声,降低过拟合风险,提升模型效果。常用的特征选择方法有:过滤法(如特征缺失率、单值率、相关系数)、包装法(如RFE递归特征消除、双向搜索)、嵌入法(如带L1正则项的模型、树模型自带特征选择)。
本节代码
模型使用L1正则项方法,本节不再做处理,可自行验证其他方法。
2.3 模型训练
神经网络模型的训练主要有3个步骤:
- 构建模型结构(主要有神经网络结构设计、激活函数的选择、模型权重如何初始化、网络层是否批标准化、正则化策略的设定)
- 模型编译(主要有学习目标、优化算法的设定)
- 模型训练及超参数调试(主要有划分数据集,超参数调节及训练)
2.3.1 模型结构
常见的神经网络模型结构有全连接神经网络(FCN)、RNN(常用于文本 / 时间系列任务)、CNN(常用于图像任务)等等。
- 输入层:为数据特征输入层,输入数据特征维数就对应着网络的神经元数。(注:输入层不计入模型层数)
- 隐藏层:即网络的中间层(可以很多层),其作用接受前一层网络输出作为当前的输入值,并计算输出当前结果到下一层。隐藏层的层数及神经元个数直接影响模型的拟合能力。
-
输出层:为最终结果输出的网络层。输出层的神经元个数代表了分类类别的个数(注:在做二分类时情况特殊一点,如果输出层的激活函数采用sigmoid,输出层的神经元个数为1个;如果采用softmax,输出层神经元个数为2个是与分类类别个数对应的;)
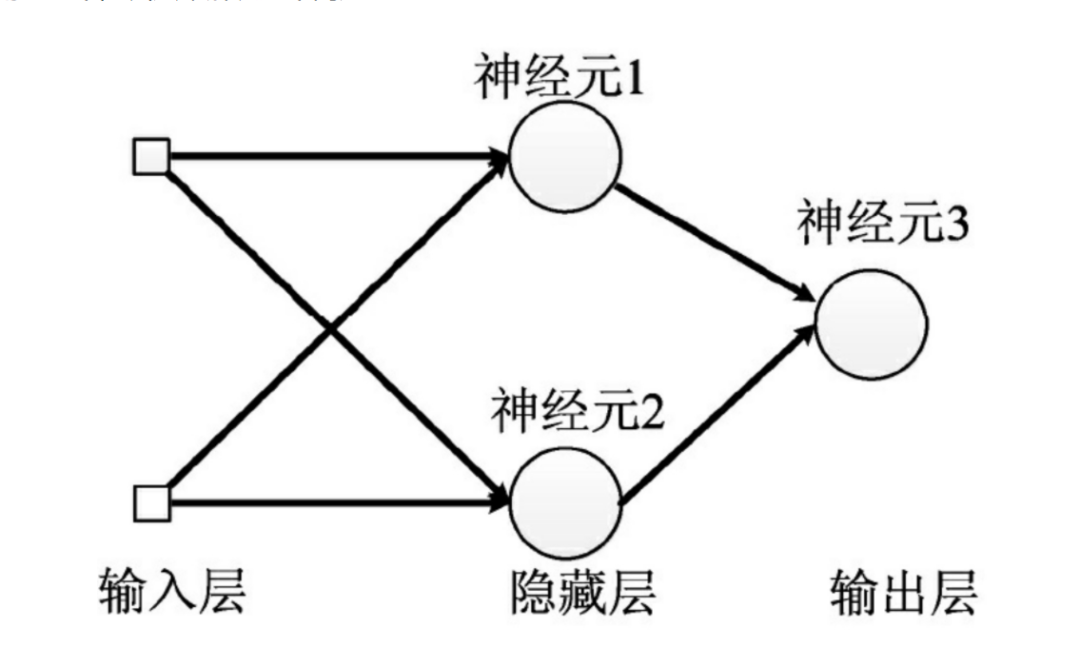
2.3.2 激活函数
根据万能近似原理,简单来说,神经网络有“够深的网络层”以及“至少一层带激活函数的隐藏层”,既可以拟合任意的函数。可见激活函数的重要性,它起着特征空间的非线性转换。对于激活函数选择的经验性做法:
- 对于输出层,二分类的输出层的激活函数常选择sigmoid函数,多分类选择softmax;回归任务根据输出值范围来确定使不使用激活函数。
- 对于隐藏层的激活函数通常会选择使用ReLU函数,保证学习效率。
2.3.3 权重初始化
权重参数初始化可以加速模型收敛速度,影响模型结果。常用的初始化方法有:
- uniform均匀分布初始化
- normal高斯分布初始化 需要注意的是,权重不能初始化为0,这会导致多个隐藏神经元的作用等同于1个神经元,无法收敛。
2.3.4 批标准化
batch normalization(BN)批标准化,是神经网络模型常用的一种优化方法。它的原理很简单,即是对原来的数值进行标准化处理: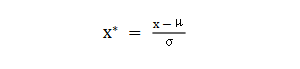 batch normalization在保留输入信息的同时,消除了层与层间的分布差异,具有加快收敛,同时有类似引入噪声正则化的效果。它可应用于网络的输入层或隐藏层,当用于输入层,就是线性模型常用的特征标准化处理。
batch normalization在保留输入信息的同时,消除了层与层间的分布差异,具有加快收敛,同时有类似引入噪声正则化的效果。它可应用于网络的输入层或隐藏层,当用于输入层,就是线性模型常用的特征标准化处理。
2.3.5 正则化
正则化是在以(可能)增加经验损失为代价,以降低泛化误差为目的,抑制过拟合,提高模型泛化能力的方法。经验上,对于复杂任务,深度学习模型偏好带有正则化的较复杂模型,以达到较好的学习效果。常见的正则化策略有:dropout,L1、L2、earlystop方法。
2.3.6 选择学习目标
机器 / 深度学习通过学习到“好”的模型去决策,“好”即是机器 / 深度学习的学习目标,通常也就是预测值与目标值之间的误差尽可能的低。衡量这种误差的函数称为代价函数 (Cost Function)或者损失函数(Loss Function),更具体地说,机器 / 深度学习的目标是极大化降低损失函数。
- 均方误差损失函数
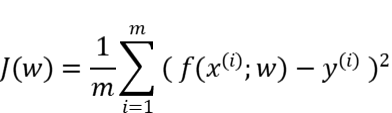
- 交叉熵损失函数
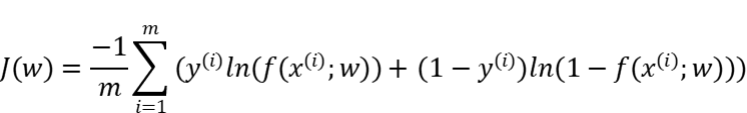 另外,还有一些针对优化难点而设计的损失函数,如Huber Loss主要用于解决回归问题中,存在奇点数据带偏模型训练的问题。Focal Loss主要解决分类问题中类别不均衡导致的模型训偏问题。
另外,还有一些针对优化难点而设计的损失函数,如Huber Loss主要用于解决回归问题中,存在奇点数据带偏模型训练的问题。Focal Loss主要解决分类问题中类别不均衡导致的模型训偏问题。
2.3.7 选择优化算法
当我们机器 / 深度学习的学习目标是极大化降低(某个)损失函数,那么如何实现这个目标呢?通常机器学习模型的损失函数较复杂,很难直接求损失函数最小的公式解。幸运的是,我们可以通过优化算法(如梯度下降、随机梯度下降、Adam等)有限次迭代优化模型参数,以尽可能降低损失函数的值,得到较优的参数值。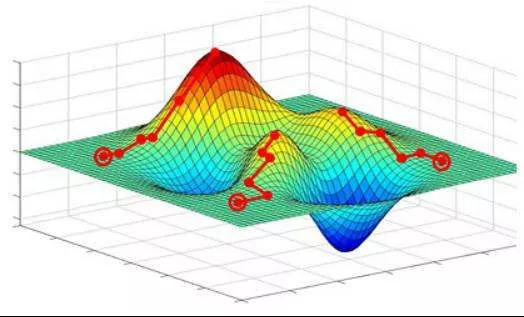
2.3.8 模型训练及超参数调试
- 划分数据集
- 超参数调试
本节代码
-
创建模型结构结合当前房价预测任务是一个经典简单表格数据的回归预测任务。我们采用基础的全连接神经网络,隐藏层的深度一两层也就差不多。通过keras.Sequential方法来创建一个神经网络模型,并在依次添加带有批标准化的输入层,一层带有relu激活函数的k个神经元的隐藏层,并对这层隐藏层添加dropout、L1、L2正则的功能。由于回归预测数值实际范围(5~50 )直接用线性输出层,不需要加激活函数。
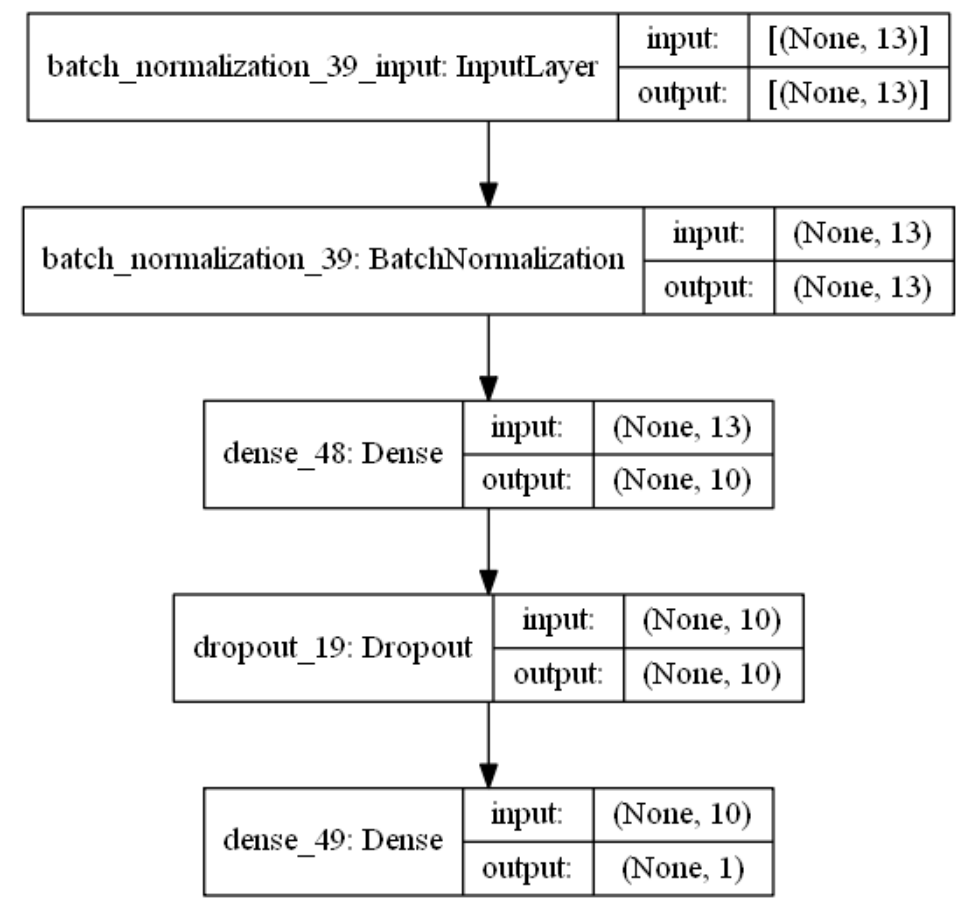
import matplotlib.pyplot as plt
%matplotlib inline
from tensorflow import random
from keras import regularizers
from keras.layers import Dense,Dropout,BatchNormalization
from keras.models import Sequential, Model
from keras.callbacks import EarlyStopping
from sklearn.metrics import mean_squared_error
np.random.seed(1) # 固定随机种子,使每次运行结果固定
random.set_seed(1)
# 创建模型结构:输入层的特征维数为13;1层k个神经元的relu隐藏层;线性的输出层;
for k in [5,20,50]: # 网格搜索超参数:神经元数k
model = Sequential()
model.add(BatchNormalization(input_dim=13)) # 输入层 批标准化
model.add(Dense(k,
kernel_initializer='random_uniform', # 均匀初始化
activation='relu', # relu激活函数
kernel_regularizer=regularizers.l1_l2(l1=0.01, l2=0.01), # L1及L2 正则项
use_bias=True)) # 隐藏层
model.add(Dropout(0.1)) # dropout法
model.add(Dense(1,use_bias=True)) # 输出层
- 模型编译设定学习目标为(最小化)回归预测损失mse,优化算法为adam
- 模型训练我们通过传入训练集x,训练集标签y,使用fit(拟合)方法来训练模型,其中epochs为迭代次数,并通过EarlyStopping及时停止在合适的epoch,减少过拟合;batch_size为每次epoch随机采样的训练样本数目。
history = model.fit(train_x,
train_y,
epochs=500, # 训练迭代次数
batch_size=50, # 每epoch采样的batch大小
validation_split=0.1, # 从训练集再拆分验证集,作为早停的衡量指标
callbacks=[EarlyStopping(monitor='val_loss', patience=20)], #早停法
verbose=False) # 不输出过程
print("验证集最优结果:",min(history.history['val_loss']))
model.summary() #打印模型概述信息
# 模型评估:拟合效果
plt.plot(history.history['loss'],c='blue') # 蓝色线训练集损失
plt.plot(history.history['val_loss'],c='red') # 红色线验证集损失
plt.show()
最后,这里简单采用for循环,实现类似网格搜索调整超参数,验证了隐藏层的不同神经元数目(超参数k)的效果。由验证结果来看,神经元数目为50时,损失可以达到10的较优效果(可以继续尝试模型增加深度、宽度,达到过拟合的边界应该有更好的效果)。

2.4 模型评估及优化
机器学习学习的目标是极大化降低损失函数,但这不仅仅是学习过程中对训练数据有良好的预测能力(极低的训练损失),根本上还在于要对新数据(测试集)能有很好的预测能力(泛化能力)。
- 评估模型误差的指标
注:如分类任务的f1-score等指标只能用于评估模型最终效果,因为作为学习目标时它们无法被高效地优化,训练优化时常用交叉熵作为其替代的分类损失函数 (surrogate loss function)。查准率P:是指分类器预测为Positive的正确样本(TP)的个数占所有预测为Positive样本个数(TP FP)的比例;查全率R:是指分类器预测为Positive的正确样本(TP)的个数占所有的实际为Positive样本个数(TP FN)的比例。F1-score是查准率P、查全率R的调和平均:
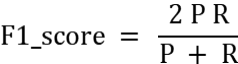
- 评估拟合效果
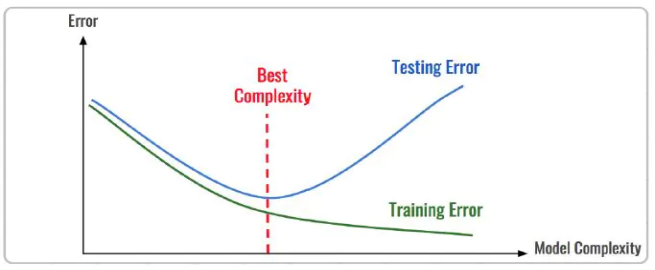
- 优化拟合效果的方法
本节代码
# 模型评估:拟合效果import matplotlib.pyplot as plt
plt.plot(history.history['loss'],c='blue') # 蓝色线训练集损失
plt.plot(history.history['val_loss'],c='red') # 红色线验证集损失
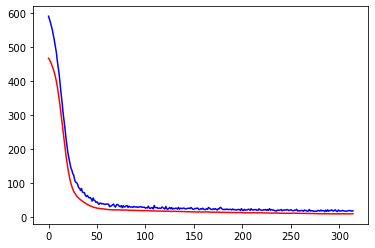 从训练集及验证集的损失来看,训练集、验证集损失都比较低,模型没有过拟合现象。
从训练集及验证集的损失来看,训练集、验证集损失都比较低,模型没有过拟合现象。
pred_y = model.predict(test_x)[:,0]
print("正确标签:",test_y)
print("模型预测:",pred_y )
print("实际与预测值的差异:",mean_squared_error(test_y,pred_y ))
#绘图表示
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置图形大小
plt.figure(figsize=(8, 4), dpi=80)
plt.plot(range(len(test_y)), test_y, ls='-.',lw=2,c='r',label='真实值')
plt.plot(range(len(pred_y)), pred_y, ls='-',lw=2,c='b',label='预测值')
# 绘制网格
plt.grid(alpha=0.4, linestyle=':')
plt.legend()
plt.xlabel('number') #设置x轴的标签文本
plt.ylabel('房价') #设置y轴的标签文本
# 展示
plt.show()
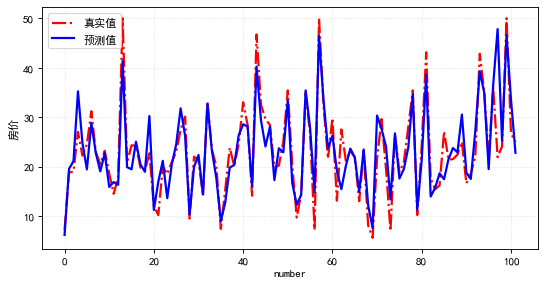
评估测试集的预测结果,其mse损失为19.7,观察测试集的实际值与预测值两者的数值曲线是比较一致的!模型预测效果较好。
2.5 模型预测结果及解释性
决策应用是机器学习最终目的,对模型预测信息加以分析解释,并应用于实际的工作领域。
本节代码
如下通过SHAP方法,对模型预测单个样本的结果做出解释,可见在这个样本的预测中,CRIM犯罪率为0.006、RM平均房间数为6.575对于房价是负相关的。LSTAT弱势群体人口所占比例为4.98对于房价的贡献是正相关的...,在综合这些因素后模型给出最终预测值。
import tensorflow as tf # tf版本<2.0
# 模型解释性
background = test_x[np.random.choice(test_x.shape[0],100, replace=False)]
explainer = shap.DeepExplainer(model,background)
shap_values = explainer.shap_values(test_x) # 传入特征矩阵X,计算SHAP值
# 可视化第一个样本预测的解释
shap.force_plot(explainer.expected_value, shap_values[0,:], test_x.iloc[0,:])









